Dalam model Structural Equation Modeling (SEM) yang menggunakan Maximum Likelihod Estimation (MLE) mengasumsikan bahwa data berdistribusi normal baik normal univariate dan juga multivariate.
To assess normality it si often helpful to examine both univariate and multivariate normality indexes. Univariate distributions can be examined for outliers and skewness and kurtosis. Multivariate distributions are examined for normality and multivariate outlier (Ulmann, 2006).
Uji normalitas ini dapat dilihat pada nilai nilai
Critical Ratio (CR) dari skewness dan kurtosisnya. Jika nilai CR antara rentang - 2.58 sampai dengan 2.58 (
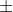
2.58) pada tingkat singnifikansi 1% (0.01), dapat disimpulkan bahwa bahwa data berdistribusi normal baik univariate maupun multivariat. Hasil uji normalitas dengan AMOS dapat dilihat di bawah ini.
 |
| Uji Normal Pada Output AMOS |
Pada hasil output di atas, nilai critical ratio (CR) skewness dan kurtosis dari variabel (indikator) X1,X2, X3, X4, X5, X6, X12, X13 dan X14 menunjukkan hasil tidak ada variabel (indikator) dengan nilai CR kurang (-) 2.58 dan lebih (+) 2.58. Nilai CR dari skewness terkecil pada indikator X3 yaitu -2.331 dan tertinggi pada X2 sebesar -0.149. Demikian juga nilai CR dari kurtosis tertinggi pada indikator X6 sebesar 1.276 dan terendah X4 (-1.365). Karena nilai CR terletak diantara -2.58 dan 2.58 membuktikan bahwa variabel tersebut normal univariate. Sedangkan nilia kurtosis multivariate yang diperoleh sebesar 4.747 dengan nilai CR 2.386. Sehingga dapat disimpulkan bahwa data berdistribusi normal multivariate.
Untuk model dengan Lisrel dapat dilihat pada tabel uji normal di bawah ini.
 |
| Uji Normal Pada Output Lisrel |
Pada output normalitas dengan Lisrel pengujian dilakukan dengan mengubah nilai menjadi Z standar sehingga diperoleh nilai Z score dan P-value pada skewness dan kurtosisnya. Kriteria data berdistribusi normal jika p-value dari chi-square yang didapat lebih besar dari 0.05 maka data berdistribusi normal. Terlihat bahwa nilai p-value chi-square semua variabel X1, X2, X3, X4, X5, X6, X12, X13 dan X14 memiliki nilai p-value lebih besar dari 0.05 maka dapat disimpulkan bahwa data berdistribusi normal univariate.
Sedangkan uji normal multivariate dapat dilihat pada nilai p-value dari chi-square skewness dan kurtosis. nilai Chi-square yang dihasilkan sebesar 49.058 dan p-value 0.000. Nilai ini memberikan bukti bahwa data tidak berdistribusi normal multivariate karena nilai p-value 0.000 lebih kecil dari 0.05
Referensi :
Byrne, B.M.(1998).Structural Equation Modeling With Lisrel, Prelis and Simplis: Basic Concepts, Applications and Programing. New Jersey: Lawrence Erlabaum Associates,Inc
Raykov,T and Marcoulides, G.A.(2006).A First Course in Structural Equation Modeling 2nd. New Jersey London: Lawrence Erlbaum Associates
Ulmann,J.B.(2006).Structural Equation Modeling: Reviewing the Basics and Moving Forward.Journal of Personality Assesment, 87 (1), 35 -50.
Vieira,A,L.(2011).Interactive LISREL in Practice Getting Started with a Simplis Approach. London New York: Springer Science





