Uji Inner Model PLS Path-Modeling

Uji Inner Model dilakukan untuk menguji hubungan antara konstruk eksogen dan endogen yang telah dihipotesiskan sebelumnya. untuk menghasilkan nilai-nilai pengujian inner model, langkah di SmartPLS dilakukan dengan metode bootstraping. Uji Iner Model disebut juga dengan uji struktural. Ada beberapa uji dalam Inner Model yaitu :

 

Nilai

seperti halnya pada regresi linier yaitu kemampuan konstruk eksogen menjelaskan variasi pada konstruk endogen. Ada 3 kriteria nilai yaitu : 0.67 artinya  baik, 0.33 artinya moderat dan 0.19  (lemah).

Estimasi Koefisien Jalur

Nilai estimasi  koefisien jalur antara konstruk harus memiliki nilai yang signifikan. Signifikansi hubungan dapat diperoleh dengan prosedur Bootstrapping atau Jacknifing. Nilai yang dihasilkan berupa nilai t-hitung yang kemudian dibandingkan dengan t-tabel. Apabila nilai t-hitung > t-tabel (1.96) pada taraf signifikansi ( 5%) maka nilai estimasi koefisien jalur tersebut signifikan. Jika pakai taraf signifikansi 10%, nilai t-valuel 1,65. Sedangkan taraf signifikansi 1% maka nilai t-value 2,58.

Effect Size ()
Effect size dilakukan untuk mengetahui perubahan nilai pada konstruk endogen. Perubahan nilai menunjukan pengaruh konstruk eksogen terhadap konstruk endogen apakah memiliki pengaruh yang subtantif. Nilai effect size 0,02 kategori kecil, 0,15 masuk kategori menengah dan 0,35 kategori besar.
Formula effect size (),

Rumus Effect size

Dimana :
= Nilai yang diperoleh ketika konstruk eksogen dimasukkan ke model
= Nilai yang diperoleh ketika konstruk eksogen dikeluarkan dari model.

Relevansi Prediksi ()

Nilai berguna untuk validasi kemampuan prediksi model. Model ini hanya cocok dilakukan pada konstruk endogen yang mempunyai indikator reflektif. Nilai relevansi prediksi jika < 0 menunjukkan konstruk laten eksogen baik sebagai variabel penjelas yang mempu memprediksi konstruk eksogennya. Uji ini dikenal dengan uji Stone Geisser.

Formula uji 

Uji Stone Geisser

Dimana, D adalah Omission Distance, E = sum of squares of prediction errors, O adalah sum of squares of observation. Nilai diatas nol membuktikan bahwa model mempunyai prediksi relevansi.

Goodness of Fit (GoF)
Pengujian ini dilakukan untuk validasi model secara keseluruhan yaitu gabingan inner model dan outer model. Nilai GoF diperoleh dari average communalities index dikalikan dengan model. Formula uji seperti dibawah ini :

Uji GoF

Dimana :
adalah average communalities

adalah rata-rata nilai

Baca juga :

1. Mengenal Generalized Structured Component Anaysis

2. Uji Outer Model Pada PLS

3. Model Multi Group Analysis MGA

Referensi :

Ghozali, I. (2011). Structural Equation Modeling Metode Alternatif dengan Partial Least Square PLS edisi 3. Semarang : Badan Penerbit Universitas Diponegoro

Henseller, J.,Ringle,C.M and Sinkovics.R.R. (2009). The Use of Partial Least Squares Path Modeling in International Marketing : Advances in International Marketing (20).pp.277-319.

Lohmoller,J.B. (1989). Latent Variables path Modeling with partial Least Squares. Berlin, Heidelberger : Springer

Michael, H., and Andreas, M.K. (2004). A Beginner's Guide to Partial Least Square Analysis. Lawrence Erlbaum Association, Inc.

Vincenzo, et al. (2010). Handbook of Partial Least Square. Berlin, Heidelberg : Springer-Verlag.

Uji Outer Model Pada PLS-Path Modeling

Dalam model SEM yang berbasis varian atau PLS-Path Modeling, model ini terdiri dari Outer model  (model pengukuran) dan Inner model (model structural ). Dengan demikian evaluasi  model pada PLS-PM juga terdiri 2 tahap yaitu evaluasi outer model dan Inner Model. Hal yang perlu diperhatikan dalam menggunakan PLS-PM adalah tidak adanya suatu kriteria statistik yang mampu menilai secara keseluruhan suatu model sehingga peneliti tidak mampu melakukan analisa inferensi untuk menguji kelayakan model. Sebagai alternatif, uji nonparametrik melalui metode re-sampling seperti Jackknifing dan Bootstrapping bisa digunakan pada estimasi suatu model yang dihasilkan.

 

OUTER MODEL

Pada outer model kita kenal 2 tipe/jenis hubungan indikator pada konstruknya, maka pengujian dilakukan sesuai dengan bentuk indikatornya yaitu indikator reflektif dan indikator formatif.

• INDIKATOR REFLEKTIF

Loading Faktor

Nilai ini menunjukan korelasi antara indikator dengan konstruknya. Indikator dengan nilai loading yang rendah menunjukan bahwa indikator tersebut tidak bekerja pada model pengukurannya. nilai loading yang diharapkan > 0.7.

Cross Loading
Nilai ini merupakan  ukuran lain dari validitas diskrimanan. Nilai yang diharapkan bahwa setiap indikator memiliki loading lebih tinggi untuk konstruk yang diukur dibandingkan dengan nilai loading ke konstruk yang lain.

Composite Reliability

Nilai ini menunjukan internal consistency yaitu nilai composite reliability yang tinggi menunjukan nilai konsistensi dari masing-masing indikator dalam mengukur konstruknya. Nilai CR diharapkan > 0.7.

Formula Composite Reliability :

Rumus Composite Reliability

Dimana  adalah component loading ke indikator dan  .

Average Variance Extracted (AVE)
Nilai AVE digunakan untuk mengukur banyaknya varians yang dapat ditangkap oleh konstruknya dibandingkan dengan variansi yang ditimbulkan oleh kesalahn pengukuran. Nilai AVE harus lebih besar (> 0.5). Formula AVE :

Rumus AVE

Dimana  adalah component loading ke indikator dan  

• INDIKATOR FORMATIF

Pada model hubungan formatif, outer weight (penimbang) setiap indikator dbandingkan satu dengan yang lain untuk menentukan indikator yang memberikan kontribusi terbesar dalam satu konstruk. Pada alpha 5 % indikator dengan penimbang terkecil (t-statistik > 1.96). Selain signifikansi nilai weight, evaluasi dilakukan apakah terdapat multikolinieritas pada indikatornya. Untuk mengujinya dengan mengetahui nilai Variance Inflation factor (VIF). Nilai VIF < 10 mengindikasikan tidak terdapat multikolinieritas.

Dalam pengujian nilai weight akan sering didapatkan nilai weight yang tidak signifikan, dengan menghilangkan indikator satu indikator formatif tersebut akan menjadi masalah yang sangat serius karena akan mengubah makna dari konstruk formatif tersebut. Sebagai solusinya, jika nilai weight tidak signifikan dan nilai loading faktor > 0.5 maka indikator tersebut masih bisa dipertahankan. tetapi jika nilai weight tidak signifikan dan nilai loading faktor < 0.5, maka indikator tersebut dapat dikeluarkan dari model dengan persyaratan dukungan teori yang ada. 

Ketidaksignifikansi weight ini dapat disebabkan dari problem multikolinieritas, banyaknya indikator dan adanya nilai weight positif dan negatif (suppresor effect).

Baca juga :

1. Peranan Mediator Dalam PLS

2. Uji Inner Model dalam PLS

3. Model Multi Group Analysis MGA

Referensi :

Ghozali, I. (2011). Structural Equation Modeling Metode Alternatif dengan Partial Least Square PLS edisi 3. Semarang : Badan Penerbit Universitas Diponegoro

Henseller, J.,Ringle,C.M and Sinkovics.R.R. (2009). The Use of Partial Least Squares Path Modeling in International Marketing : Advances in International Marketing (20).pp.277-319.

Lohmoller,J.B. (1989). Latent Variables path Modeling with partial Least Squares. Berlin, Heidelberger : Springer

Michael, H., and Andreas, M.K. (2004). A Beginner's Guide to Partial Least Square Analysis. Lawrence Erlbaum Association, Inc.

Vincenzo, et al. (2010). Handbook of Partial Least Square. Berlin, Heidelberg : Springer-Verlag.

Uji McNemar

Uji McNemar diperkenalkan oleh seorang ahli psikologi bernama Quinn McNemar pada tahun 1947. Uji ini digunakan untuk penelitian yang membandingkan sebelum dan sesudah peristiwa/treatment dimana tiap objek digunakan sebagai pengontrol dirinya sendiri ( i.e. evaluating repeated measurements of the same objects using them as their own control). Uji dilakukan pada 2 kelompok sampel yang berhubungan, skala pengukurannya berjenis nominal (binary respon) dan untuk crosstabulasi 2x2.

Formula uji MacNemar sebagai berikut :

Rumus McNemar

Dimana :

  = Nilai khai-kuadrat hasil perhitungan
A    = Objek yang menampilkan perubahan jawaban dari positif menjadi negatif
D    = Objek yang menampilkan perubaha jawaban dari negatif menjadi positif
2     = konstanta

Contoh Kasus

Diambil sampel 50 orang, mereka diminta untuk mennetukan pemlihan Kepala Desa yang akan dipilihnya. Data diambil sebelum dan sesudah debat dari 2 calon Kepala Desa. Calon A diwakili angka 1 dan calon B diwakili angka 2. Ingin diketahui apakah terdapat perbedaan atau perubahan pilihan terhadap calon Kepala Desa setelah debat dilakukan ? Data sebagai berikut :

Data Hasil Debat Calon Kepala Desa

Langkah-langkah SPSS :

1. Klik Analyze > Nonparametrik Test > 2 Related samples
2. Masukkan kedua variabel ke dalam kolom Test Pairs List
3. Pilih Mcnemar, OK

Hipotesis :

H0 = Tidak terdapat perubahan yang signifikan pemilihan kepala desa sebelum dan sesudah debat

H1 = terdapat perubahan yang signifikan pemilihan Kepala Desa sebelum dan sesudah debat.

Kroteria uji : Tolak H0 jika nilai p-value < 0.05.

Hasil output SPSS terlihat di bawah ini.

Hasil Uji McNermar

Hasil Output SPSS di atas, nilai Chi-square sebesar 21.841 dan signifikansi p-value sebesar 0.000. Karena nilai sig.p-value 0.000 < 0.05 maka tolak hipotesis nol yang artinya ada perubahan yang signifikan pemilihan kepala desa sebelum dan sesudah debat dilakukan.

Baca juga :

1. Uji Friedman

2. Uji Q Cochran

3. Uji Sign Test

Referensi :

Elliot,A.C and Woodward,W.A. (2007). Statistical Analysis Quick References Guidebook: with SPSS Example.London New Delhi : Sage Publications

Field,A. (2009). Discovering Statistics Using SPSS 3rd. London : Sage Publications

Ho, Robert. (2006). Handbook of Univariate and Multivariate Data Analysis and Interpretation with SPSS.London New York : Chapman & Hall CRC

Landau,S and Everits,B.S. (2004).A Handbook of Statistical Analysis Using SPSS. London New York Washington : CRC Press LLC

Muijs,D. (2004). Doing Quantitative research In Education. London California : Sage Publications

Yamin,S dan Kurniawan,H. (2009). SPSS Complete : Teknik Analisis Statistik Terlengkap dengan Sofware SPSS. Jakarta : Salemba Infotek

UJI FRIEDMAN

Pengujian dengan uji Friedman sama sepertidalam uji analisis dua arah dalam statistik parametrik. Uji ini diperkenalkan oleh Milton Friedman tahun 1937 dan termasuk dalam uji nonparametrik yang tidak membutuhkan asumsi distribusi normal dan varians populasi tidak diketahui.  Skala data yang digunakan dapat berupa ordinal. Uji Friedman merupakan alternatif yang dilakukan apabila pengujian dalam ANOVA tidak terpenuhi asumsi-asumsi seperti tersebut di atas. Setiap sampel mendapatkan perlakukan yang berbeda (repeated measurement). Pegambilan data pada setiap sampel dilakkan sebelum (pre test) dan sesudah (post test).

Formula uji Friedman

Rumus Uji Friedman

Dimana :

   = Nilai khai-kuadrat jenjeng dua arah Friedman
n      = jumlah sampel
k      = banyaknya kelompok sampel
1,3, 12 = konstanta

Contoh kasus.

Suatu metode diet penurunan berat badan yaitu meode DASH (Dietary Approaches to Stop Hipertension) diuji coba terhadap 10 orang sebagai sampel. metode ini bertujuan menurunkan tekanan darah. Pelaku diet tidak berpantang terhadap makanan dan hanya memperbanyak sayuran dan buah-buahan. Untuk menguji apakah metode ini efektif menurunkan berat badan, dilakukan uji coba terhadap 10 orang. Pengukuran berat badan dilakukan sebelum program diet, 1 minggu melakukan program diet DASH dan 2 minggu kemudian. Apakah terdapat perbedaan antara ketiga kelompok sampel tersebut? Data sampel sebagai berikut :

Data Sampel

Langkah-langkah dalam SPSS

Pada langkah pertama, akan diuji normalitas data dengan uji Kolmogorov Smirnov. Hasilnya sebagai berikut.

Uji Normalitas

Pada tabel uji Kolmogorov-Smirnov di atas, nilai signifikansi pada sampel sebelum diet sebesar (0.152), minggu 1 (0.002) dan minggu 2 (0.200). Hanya kelompok sampel sebelum diet dan sampel minggu 2 yang berdistribusi normal sedangkan kelompok sampel minggu 1 tidak berdistribusi normal. Oleh karena tidak terpenuhi asumsi normal pada semua kelompok sampel maka digunakan uji Friedman.

Langkah-langkah :

• Analyze Pilih Nonparametrics kemudian K Related  Samples
• Masukkan variabel Sebelum diet, Minggu 1 dan Minggu 2 ke Test Variables
• Pada pilihan test type centang pilihan Friedman
• Pada menu Statistics, centang pilihan Descriptive, kemudian OK

Langkah Uji Friedman

 Hasil Output SPSS sebagai berikut.

Nilai Mean Rank

Nilai rata-rata rank berat badan merupakan nilai bukan sebenarnya, tetapi dilakukan rangking terhadap data aktual. Nilai mean rank sebelum diet sebesar 2.40 pada minggu 1 nilai mean rank turun menjadi 2.25 sedangkan pada minggu 2 nilai mean rank turun lagi menjadi 1.35.

Nilai Chi-Square

Hasil uji Friedman, nilai chi-square sebesar 6,973. Nilai df=2 (k-1), dimana k adalah banyaknya kelompok sampel yaitu 3 sampel, sedangkan nilai signifikansi p-value 0,031. Karena nilai p-value 0,031 lebih kecil dari 0,05 maka kesimpulannya adalah terdapat perbedaan nilai rata-rata rank antara sebelum diet, diet minggu 1 dan diet minggu 2.

Untuk menguji atau membandingkan antara 2 kelompok, misalnya sampel sebelum diet dengan diet minggu 1, sebelum diet dan minggu 2 atau diet minggu 1 dengan minggu 2 dapat dilakukan dengan uji Post Hoc.

Baca juga :

1. Uji sign test

2. Uji Run test

3. Uji Q-Cochran

Referensi :

Elliot,A.C and Woodward,W.A. (2007). Statistical Analysis Quick References Guidebook: with SPSS Example.London New Delhi: Sage Publications

Field,A. (2009). Discovering Statistics Using SPSS 3rd. London: Sage Publications

Ho, Robert. (2006). Handbook of Univariate and Multivariate Data Analysis and Interpretation with SPSS.London New York: Chapman & Hall CRC

Landau,S and Everits,B.S. (2004).A Handbook of Statistical Analysis Using SPSS. London New York Washington: CRC Press LLC

Muijs,D. (2004). Doing Quantitative research In Education. London California: Sage Publications

Yamin,S dan Kurniawan,H. (2009). SPSS Complete : Teknik Analisis Statistik Terlengkap dengan Sofware SPSS. Jakarta : Salemba Infotek

Analisis Chi Square

Uji Chi-square atau qai-kuadrat digunakan untuk melihat ketergantungan antara variabel bebas dan variabel tergantung berskala nominal atau ordinal. Prosedur uji chi-square menabulasi satu atau variabel ke dalam kategori-kategori dan menghitung angka statistik chi-square. Untuk satu variabel dikenal sebagai uji keselarasan atau goodness of fit test yang berfungsi untuk membandingkan frekuensi yang diamati (fo) dengan frekuensi yang diharapkan (fe). Jika terdiri dari 2 variabel dikenal sebagai uji independensi yang berfungsi untuk hubungan dua variabel. Seperti sifatnya, prosedur uji chi-square dilkelompokan kedalam statistik uji non-parametrik.

 

 

Semua variabel yang akan dianalisa harus bersifat numerik kategorikal atau nominal dan dapat juga berskala ordinal. Prosedur ini didasarkan pada asumsi bahwa uji nonparametrik tidak membutuhkan asumsi bentuk distribusi yang mendasarinya. Data diasumsikan berasal dari sampel acak. Frekuensi yang diharapkan (fe) untuk masing-masing kategori harus setidaknya :

Tidak boleh lebih dari dua puluh (20%) dari kategori mempunyai frekuensi yang diharapkan kurang dari 5. Jika hal diatas tersebut terjadi dan tabel silang 2x2 maka gunakan uji "Fisher Exact ".
Ada beberapa ketentuan yang berlaku pada uji chi-square antara lain:

1. Jika tabel silang 2x2 dan tidak ada nilai expected (harapan) < 5, maka uji sebaiknya : Continuity Correction.
2. Jika tabel silang 2x2 dan ada nilai expected (harapan) < 5, maka uji sebaiknya : Fisher Exact Test.
3. Jika tabel silang lebih dari 2x2 misal 2x3, 3x3, 3x4, maka uji sebaiknya : Pearson Chi Square.
4. Untuk uji Likelihood Ratio dan Linear by linear Association digunakan lebih spesifik, misal analisis pada bidang epidemiolog dan juga untuk mengetahui hubungan linier dua kategorik.
   

Formula uji Chi Square :

Rumus Chi-Square

Dimana :

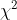
= Nilai khai-kuadrat
 fo = frekuensi observasi/pengamatan
fe = frekuensi ekspetasi/harapan

 

Contoh kasus

Perusahaan penyalur alat elektronik AC ingin mengetahui apakah ada hubungan antara gender dengan sikap mereka terhadap kualitas produk AC. Untuk itu mereka meminta 25 responden mengisi identitas mereka dan sikap atau persepsi mereka terhadap produknya.

Permasalahan : Apakah ada hubungan antara gender dengan sikap terhadap kualitas AC?

Hipotesis :

• H0 = Tidak ada hubungan antara gender dengan sikap terhadap kualitas AC
• H1 = Ada hubungan antara gender dengan sikap terhadap kualitas AC

Tolak hipotesis nol (H0) apabila nilai signifikansi chi-square < 0.05 atau nilai chi-square hitung lebih besar (>) dari nilai chi-square tabel.

Data dari keduapuluh lima responden dapat dilihat pada tabel di bawah ini.

Data Sikap Responden

Ket. : Gender : 1 = Laki-laki; 2 = Wanita, Sikap: 1 = berkualitas, 2 = Tidak berkualitas

Langkah-langkah Chi-Square dengan SPSS

1. Analyze > Descriptive Statistics > Crosstab
2. Masukkan variabel Gender ke dalam kotak Row
3. MAsukkan variabel Sikap ke dalam kotak Column
4. Klik untuk pilihan Statistics
5. Pilih menu Chi-square, tekan Continue
6. Pilih Cell, Observed, tekan Continue
7. Klik Ascending, tekan Continue
8. Tekan OK

Hasil output Chi-Square dengan SPSS

Case Processing Summary

Pada tabel case processing summary diatas menunjukkan bahwa input data ada 25 responden  dan tidak ada data yang tertinggal.

Gender*Sikap

Pada tabel crossstabulasi antara gender*sikap di atas bahwa gender laki-laki berjumlah 12 responden. Dari 12 responden laki-laki bersikap/menganggap berkualitas sedangkan 5 responden bersikap tidak berkualitas. Sedangkan 13 responden  bergender wanita yang menganggap produk AC berkualitas sebanyak 6 responden dan yang bersikap tidak berkualitas ada 7 responden.

Hasil Uji Chi-Square test

Pada tabel menunjukan bahwa tidak ada (0%) cell expected kurang dari 5. Nilai Pearson chi-square test di atas dapat diketahui bahwa nilai signifikansi p-value sebesar 0.543 dan nilai chi-square sebesar 0.371. Karena tabel silang (cross tabulation) 2x2 dan 0% cell expected  (< 5), maka menggunakan nilai continuity correction. Pada nilai continuity correction sebesar 0.043 dan signifikansi p-value 0.835 (>0.05) maka hipotesis null (H0) diterima yang berarti bahwa tidak ada hubungan yang signifikan antara gender dengan sikap terhadap kualitas AC.

Baca Juga :

1. Analisis Deskriptive Crosstab

2. Korelasi Pearson

3. Analisis Korelasi dan Asosiasi

Referensi :

Dunn,O.J and Clark,V.J. (2009). Basics Statistics A Primer for the Biomedical Sciences  4 Edition.New Jersey: A John Wiley & Sons

Field, A. (2009). Discovering Statistics Using SPSS 3rd. London : Sage Publication

Mehta,C.R and Patel,N.R. (1996). SPSS Exact tests. Chicago: SPSS Inc

Riyanto,A. (2010). Pengolahan Dan Analisis Data Kesehatan. Yogyakarta: Nuha Medika

Triola,M.F. (2012). Elementary Statistics 11th. London: Pearson Education Inc