Uji Kruskall-Wallis sama halnya seperti analisis varians (ANOVA) akan tetapi uji ini tidak memerlukan adanya asumsi distribusi normal. Prosedur pengujian Kruskall-Wallis dilakukan untuk menganalisa data tiga atau lebih sampel independen. Metode ini diperkenalkan oleh dua pakar statistika William H. Kruskall dan Allen Wallis pada tahun 1952.
Formula sebagai berikut :
}X\sum_{k-1}^{k}\frac{R_{k}^{2}}{N_{k}}-3\left&space;(&space;n+1&space;\right&space;)) |
| Rumus Uji Krusskal Wallis |
Dimana :
H = nilai hasil perhitungan
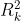
= kuadrat jumlah jenjang secara keseluruhan
n = jumlah sampel keseluruhan
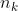
= jumlah sampel pada tiap kelompok
12, 1, dan 3 = merupakan konstanta.
Contoh kasus
Seorang manajer penjualan mesin traktor pertanian ingin mengetahui apakah penjualan traktor di cabang toko yang berada di tiga kota yaitu Kebumen, Solo dan Semarang terdapat perbedaan dalam penjualan mesin traktor. Data penjulan ketiga cabang toko disajikan sebagai berikut :
 |
| Data Penjualan di 3 Kota |
Keterangan.
1 = Kebumen
2 = Solo
3 = Semarang
Hipotesis
H0 = Tidak ada perbedaan penjualan traktor pertanian antara kota kebumen, Solo dan Semarang
H1 = Ada perbedaan penjualan traktor pertanian antara kota Kebumen, Solo dan Semarang
Langkah-langkah pengujian dengan Sofware Minitab.
- Stat > Nonparametrics > Kruskal-Wallis
- Masukkan variabel Penjualan ke kolom Response dan Kota ke kolom Factor
- Kemudian OK
Hasil output
 |
| Hasil Uji Kruskal Wallis |
Hasil output menunjukkan bahwa di kota Kebumen nilai median dari penjualan traktor sebesar 98 unit, average rank (rata-rata) sebesar 30,7 dan nilai Z (normal) 0.06. Untuk penjualan di kota Solo nilai median penjualan traktor 96 unit, average rank (rata-rata) 26,9 dan nilai Z -1.13. Sedangkan penjulan dikota Semarang nilai median 101,5 unit, average rank 33,5 dan nilai Z sebesar 1.07.
Nilai H yang didapat sebesar 1,61 dan probabilitas (p) sebesar 0.447. Kriteria pengujian dengan membandingkan nilai H (chi-square) statistik dengan chi-square tabel. Jika nilai chi-square statistik (H) < chi-square tabel maka terima H0 (Hipotesis null). Nilai chi-square tabel pada taraf signifikansi 5% dan df (degree of freedom) 2 sebesar 5,991. Karena nilai chi-square statistik (H) 1,61 < 5,991 chi-square tabel maka terima hipotesis nul (H0). Hal ini didukung juga dengan nilai (p) yang di peroleh sebesar 0.447 > 0.05. Kesimpulan : Tidak ada perbedaan penjualan traktor pertanian antara kota Kebumen, Solo dan Semarang.
Alan Bryman and Duncan Cramer. (2005). Quantitatif Data Analysis with Minitab : A guide for Sosial Scientists. London : Taylor and Francis e-library.
Elliot,A.C and Woodward,W.A. (2007). Statistical Analysis Quick
References Guidebook: with SPSS Example.London New Delhi : Sage
Publications
Field,A. (2009). Discovering Statistics Using SPSS 3rd. London : Sage Publications
Fikri Lukiastusi dan Muliawan Hamdani. (2012). Statistika Non Parametris : Aplikasinya dalam Bidang Ekonomi dan Bisnis.Yogyakarta : CAPS.
Ho,
Robert. (2006). Handbook of Univariate and Multivariate Data Analysis and
Interpretation with SPSS.London New York : Chapman & Hall CRC
Neil. J Salkind. 2007. Encyclopedia Measurement and Statistics. Volume 1. Sage Publications.
Landau,S and Everits,B.S. (2004).A Handbook of Statistical Analysis Using SPSS. London New York Washington : CRC Press LLC
Muijs,D. (2004). Doing Quantitative research In Education. London California : Sage Publications
Yamin,S
dan Kurniawan,H. (2009). SPSS Complete : Teknik Analisis Statistik
Terlengkap dengan Sofware SPSS. Jakarta : Salemba Infotek




Tidak ada komentar:
Posting Komentar